$x$と$y$についての関数を$y=F(x)$と表す代わりに, 第三の変数$t$を用いて, $$x=f(t),\qquad y=g(t)\tag{1}$$ として, 関数$y=F(x)$または曲線$y=F(x)$を間接的に表すことがある. このとき, (1)を$y=F(x)$の媒介変数表示といい, $t$を媒介変数とかパラメータと呼ぶ.
- 媒介変数表示$\begin{cases}x=t+2 \\ y=t^2+1\end{cases}$は, 2次曲線$y=(x-2)^2+1$を表している.
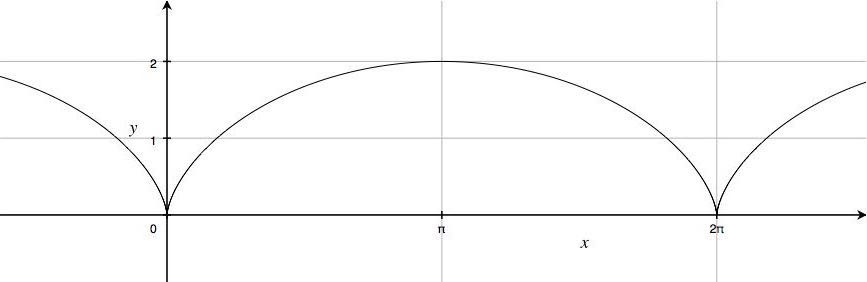
- 媒介変数表示
$\begin{cases}x=t-\sin t \\ y=1-\cos t\end{cases}$は,
サイクロイド(擺線, cycloid)と呼ばれる下の図の曲線を表している.
これは, 円を直線に沿って転がしたときの円周上の一点が描く曲線である.
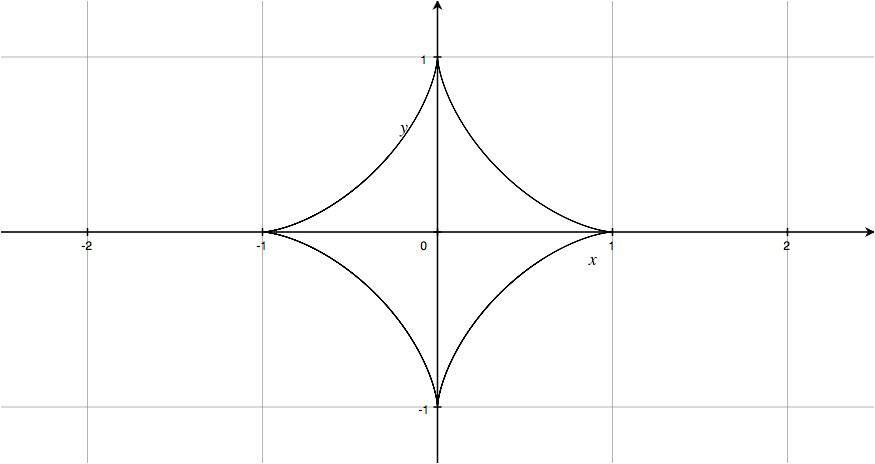
- 媒介変数表示
$\begin{cases}x=\cos^3 t \\ y=\sin^3 t\end{cases}$は,
アステロイド(astroid)と呼ばれる下の図の曲線を表している.
これは, 大円の内側に沿って小円を転がしたときの円周上の一点が描く曲線である.
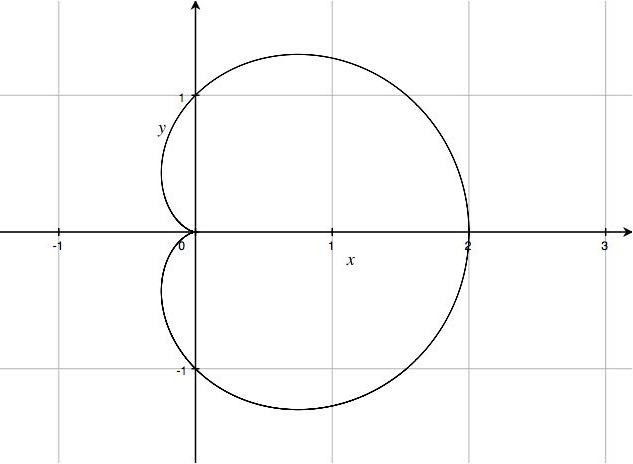
- 媒介変数表示
$\begin{cases}x=(1+\cos t)\cos t \\ y=(1+\cos t)\sin t\end{cases}$は,
カージオイド(心臓形, cardioid)と呼ばれる下の図の曲線を表している.
これは, 円の外側に沿って同じ大きさの別の円を転がしたときの円周上の一点が描く曲線である.
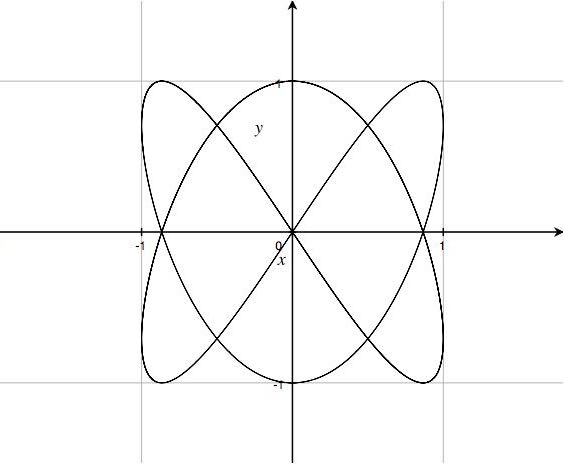
- 媒介変数表示
$\begin{cases}x=\sin(at+d) \\ y=\sin bt\end{cases}$は,
リサジュー曲線(Lissajous curve)と呼ばれる下の図の曲線を表している.
これは, $x$方向にも$y$方向にも単振動する点の描く曲線である.
- 媒介変数表示
$\begin{cases}x=\cos t+t\sin t \\ y=\sin t-t\cos t\end{cases}$は,
インボリュート(伸開線, involute)と呼ばれる下の図の曲線を表している.
これは, 回転しない固定された円形のリールに巻かれた糸を弛まないように引きほどくときに端点が描く曲線である.
定理 媒介変数表示$x=f(t), y=g(t)$で関数$y=F(x)$が表されているとき, $f(t), g(t)$が微分可能で$f^\prime(t)\ne 0$ならば, $$F^\prime(x)=\dfrac{g^\prime(t)}{f^\prime(t)}\tag{2}$$ が成り立つ. この式は $$\dfrac{dy}{dx}=\dfrac{\left(\dfrac{dy}{dt}\right)}{\left(\dfrac{dx}{dt}\right)}\tag{3}$$ とも書かれる.
証明 $y=F(x)$に$y=g(t), x=f(t)$を代入すれば$g(t)=F(f(t))$である. この式の両辺を$t$について微分すれば, $$g^\prime(t)=F^\prime(f(t))f^\prime(t)$$ を得る. この両辺を$f^\prime(t)$で割り, $x=f(t)$を用いれば, $F^\prime(x)=F^\prime(f(t))=\dfrac{g^\prime(t)}{f^\prime(t)}$が得られる.
例 $x=t+2$, $y=t^2+1$という媒介変数表示について, $\dfrac{dx}{dt}=1$, $\dfrac{dy}{dt}=2t$であるが, $t=x-2$なので, 定理の(3)より, $\dfrac{dy}{dx}=\dfrac{2t}{1}=2(x-2)$を得る. これは媒介表示されている曲線$y=(x-2)^2+1$を直接微分しても簡単に計算することができる.
例
$x=t-\sin t$, $y=1-\cos t$という媒介変数表示によるサイクロイドについて,
$\dfrac{dx}{dt}=1-\cos t, \dfrac{dy}{dt}=\sin t$なので,
定理の(3)より, $\dfrac{dy}{dx}=\dfrac{\sin t}{1-\cos t}$が得られる.
さらに$t=\dfrac{\pi}{3}$における点$P$の接線の方程式を求めてみる.
点$P$の座標を$(u,v)$とおけば,
$$u=\dfrac{\pi}{3}-\sin\dfrac{\pi}{3}=\dfrac{\pi}{3}-\dfrac{\sqrt{3}}{2},\qquad
v=1-\cos\dfrac{\pi}{3}=\dfrac{1}{2}$$であり,
また, 接線の傾きは
$$\left.\dfrac{dy}{dx}\right|_{t=\dfrac{\pi}{3}}=\dfrac{\sin\dfrac{\pi}{3}}{1-\cos\dfrac{\pi}{3}}=\dfrac{\left(\dfrac{\sqrt{3}}{2}\right)}{\left(\dfrac{1}{2}\right)}=\sqrt{3}$$
である.
従って, $t=\dfrac{\pi}{3}$における点$P$での接線の方程式は,
$$y=\sqrt{3}\left(x-\dfrac{\pi}{3}+\dfrac{\sqrt{3}}{2}\right)+\dfrac{1}{2}$$
で与えられる.